Figure 59
i.e. 
represents the length of the arc 
.
Then by geometry the chord 
If Q be taken close to P, i.e. 
becomes
small, the length of the chord is nearly equal to the length of the arc.
If Q is indefinitely close to P, in the limit when 
, the
chord approaches to coincidence when the curve and the sum of these
chords is equal with the length of the arc.
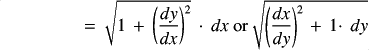
If the integration is more conveniently performed with respect to
values of y, then 
, where c and d are
limits of y.
In many cases the evaluation of the integral is difficult and requires a more advanced knowledge of the subject than is contained in this volume.
(Teach yourself calculus)